Analyse du binaire

"Main"

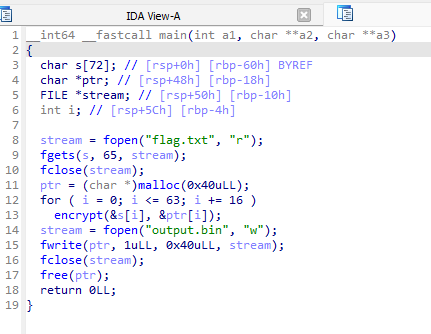
On constate très rapidement que un flag est lu, passé via une fonction de chiffrement, puis écrit dans le fichier output.bin par bloc de 16octets.

encrypt()

"Main" "Main"

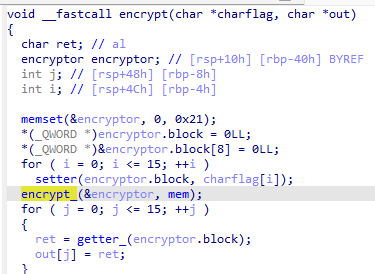
Donc nous avons une fonction encrypt() qui initialise une structure encryptor (char state[32] + block[16]) , tout est mit à 0

Une fonction setter permet de créer une double liste chainé (setter crée un bloc dans la chaine, getter en retire un)

On a donc une liste chainé de 16blocs initialisé au début avec les octets du flag. Cette liste sera vidé à la fin.

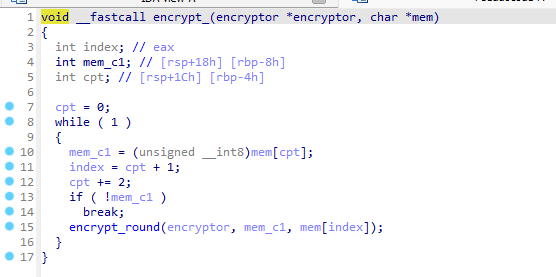
Pour encrypt_, On a une boucle qui parcourt un tableau de 2 en 2. ce tableau (mem) contient un sélécteur en premier puis une valeur.

encrypt_round

"Main"

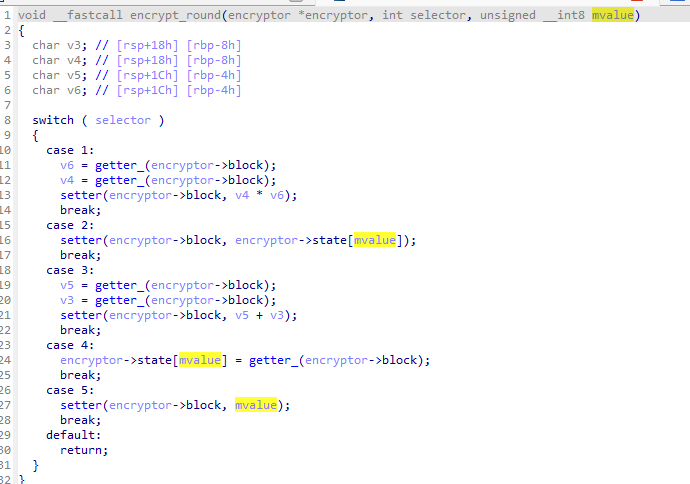
nous avons 5 choix de sélécteur :

1 : récupère 2 block de la liste chainé et set un nouveau bloc dans la liste avec la multiplication des 2
2 : set un nouveau bloc dans la liste avec la valeur contenu dans encrypto->state à l’index de mvalue
3 : idem que 1, mais c’est une addition
4 : set une value de encryptor->state à l’index mvalue via un bloc récupéré depuis la liste chainé
5 : set un block de la liste avec mvalue

Analyse de l’encryptor

En parcourant les sélécteurs dans mem, on repère la suite de choix suivant :

dans l’ordre

4 * 16
2/5 * 16
1 * 16
3 * 16

puis de manière itérative 16fois

4 (1)
2/5 * 16
1 * 16
3 * 16

puis en dernier
 
4 (1)
2 * 16

De manière générale, en suivant l’état de l’encryptor, on repère que le programme va utiliser le sélécteur 4 pour set les octets du flag dans le encryptor->state, faire une multiplication avec une clé stocké dans mem, puis ajouter le résultat jusqu’a réduire en un seul octet.

On a donc :

def encrypt():
    block_out = [0]*16
    for i in range(len(keys)):

        key = keys[i]

        f0 = flag[0] * key[0]
        f1 = flag[1] * key[1]
        f2 = flag[2] * key[2]
        f3 = flag[3] * key[3]
        f4 = flag[4] * key[4]
        f5 = flag[5] * key[5]
        f6 = flag[6] * key[6]
        f7 = flag[7] * key[7]
        f8 = flag[8] * key[8]
        f9 = flag[9] * key[9]
        f10 = flag[10] * key[10]
        f11 = flag[11] * key[11]
        f12 = flag[12] * key[12]
        f13 = flag[13] * key[13]
        f14 = flag[14] * key[14]
        f15 = flag[15] * key[15]

        d1 = f0 + f1
        d2 = f2 + f3
        d3 = f4 + f5
        d4 = f6 + f7
        d5 = f8 + f9
        d6 = f10 + f11
        d7 = f12 + f13
        d8 = f14 + f15

        cc1 = d1 + d2
        cc2 = d3 + d4
        cc3 = d5 + d6
        cc4 = d7 + d8

        ck1 = cc1 + cc2
        ck2 = cc3 + cc4

        c1 = ck1 + ck2
        block_out[i] = c1

Cet algorithme ne permet pas directement de trouver une fonction inverse (hashage, on perd de la donnée), mais sa sécurité est faible donc on peut écrire un script de solve avec z3.

#récupéré dans mem

keys = [[170, 237, 236, 93, 142, 135, 65, 255, 166, 166, 16, 91, 198, 1, 122, 253], [61, 113, 174, 90, 79, 220, 48, 235, 141, 151, 254, 40, 64, 76, 131, 127], [115, 204, 168, 225, 233, 242, 141, 102, 80, 175, 32, 117, 30, 15, 213, 91], [60, 35, 61, 255, 133, 212, 75, 110, 81, 35, 159, 111, 146, 237, 215, 142], [179, 68, 170, 215, 255, 48, 250, 58, 77, 39, 49, 22, 83, 93, 73, 96], [130, 47, 195, 93, 192, 178, 12, 43, 151, 29, 29, 55, 86, 76, 161, 55], [128, 107, 107, 112, 214, 51, 36, 132, 207, 213, 25, 166, 254, 206, 248, 98], [21, 72, 129, 228, 192, 190, 109, 203, 19, 35, 56, 202, 249, 95, 176, 159], [39, 66, 218, 115, 168, 25, 32, 137, 73, 185, 80, 213, 69, 68, 59, 16], [12, 197, 214, 249, 215, 165, 171, 176, 79, 65, 251, 16, 142, 112, 6, 17], [205, 251, 189, 70, 254, 140, 181, 213, 252, 112, 106, 243, 66, 193, 147, 180], [149, 205, 80, 192, 174, 110, 160, 121, 103, 78, 174, 90, 205, 99, 2, 174], [79, 144, 161, 243, 140, 55, 149, 18, 60, 201, 149, 216, 2, 226, 49, 81], [114, 188, 139, 5, 60, 238, 7, 114, 202, 44, 75, 118, 130, 100, 8, 91], [18, 91, 153, 190, 44, 223, 146, 193, 250, 24, 25, 51, 158, 102, 122, 164], [211, 205, 34, 52, 227, 81, 76, 70, 147, 203, 66, 176, 190, 199, 34, 48]]

waiting= open("output.bin.bak","rb").read()

from z3 import *

flag_all = ""
for block in range(0, len(waiting), 16):
    s = Solver()

    flag = [BitVec(f"f{i}",8) for i in range(16)]

    for var in flag:
        s.add(var >= 32)
        s.add(var <= 126)

    block_16b = waiting[block:block+16]

    for i in range(len(keys)):

        key = keys[i]

        f0 = flag[0] * key[0]
        f1 = flag[1] * key[1]
        f2 = flag[2] * key[2]
        f3 = flag[3] * key[3]
        f4 = flag[4] * key[4]
        f5 = flag[5] * key[5]
        f6 = flag[6] * key[6]
        f7 = flag[7] * key[7]
        f8 = flag[8] * key[8]
        f9 = flag[9] * key[9]
        f10 = flag[10] * key[10]
        f11 = flag[11] * key[11]
        f12 = flag[12] * key[12]
        f13 = flag[13] * key[13]
        f14 = flag[14] * key[14]
        f15 = flag[15] * key[15]

        d1 = f0 + f1
        d2 = f2 + f3
        d3 = f4 + f5
        d4 = f6 + f7
        d5 = f8 + f9
        d6 = f10 + f11
        d7 = f12 + f13
        d8 = f14 + f15

        cc1 = d1 + d2
        cc2 = d3 + d4
        cc3 = d5 + d6
        cc4 = d7 + d8

        ck1 = cc1 + cc2
        ck2 = cc3 + cc4

        c1 = ck1 + ck2

        s.add(c1 == block_16b[i])

    if s.check() == sat:
        model = s.model()
        flag2 = ''.join([chr(model[flag[i]].as_long()) for i in range(len(flag))])
        flag_all += flag2
    else:
        print("no solution")

    flag = None
    s = None

print(flag_all)

//ictf{S_d1dnt_5t4nd_f0r_5t4ck_b3c4u53_h3r3_I_us3d_4_L1nk3d_qu3u3}