Analyse du binaire

"Main"

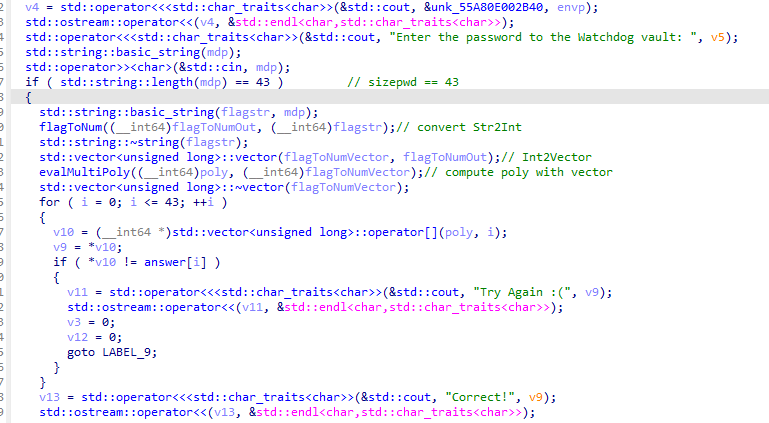
Le mot de passe est prit du stdin (size=43) Il est converti en Int puis en vecteur. Il est passé dans la fonction EvalMultiPoly qui semble calculer un polynome à partir du flag. Chaque octet est testé avec un array d’answer.

analyse de la génération de polynome

on a (en pseucode) :

computed = evalMultiPoly(flag)

def evalMultiPoly(flag):
    s = []
    for i in range(2, len(flag)+3, 1):
        s.append(evalPoly(flag, i))
    retrun s

def my_pow(a1:int, a2:int):
    if a2 == 0:
        return 1
    if a2 == 1:
        return a1
    if (a2 & 1) != 0:
        return a1 * my_pow(a1 * a1, (a2 - 1) >> 1)
    return my_pow(a1 * a1, a2 >> 1)

def evalPoly(flagVec, index):
    v4 = len(flagVec) - 1
    s = 0
    while v4 >= 0:
        v5 = len(flagVec) - v4 - 1
        v2 = flagVec[v5]
        s += v2 * my_pow(index, v4)
        v4 -= 1
    return s

Donc le binaire compute le résultat d’un polynome avec les octets du flag comme coefficient

On peut implémenter un petit script z3 pour trouver le flag :

solve

from z3 import *

def my_pow(a1:int, a2:int):
    if a2 == 0:
        return 1
    if a2 == 1:
        return a1
    if (a2 & 1) != 0:
        return a1 * my_pow(a1 * a1, (a2 - 1) >> 1)
    return my_pow(a1 * a1, a2 >> 1)

def evalPoly(flagVec, index):
    v4 = len(flagVec) - 1
    s = 0
    while v4 >= 0:
        v5 = len(flagVec) - v4 - 1
        v2 = flagVec[v5]
        s += v2 * my_pow(index, v4)
        v4 -= 1
    return s

def create_constraints(flag_vars):
    c_out = []
    length = len(flag_vars)
    for i in range(2, length + 3):
        poly_value = Sum([flag_vars[j] * my_pow(i, len(flag_vars) - 1 - j) for j in range(len(flag_vars))])
        c_out.append(poly_value)
    return c_out

def solve_flag(answer):
    solver = Solver()
    
    flag_length = 43
    #64 bit vector requis, 8bit va se faire overflow avec my_pow
    flag_vars = [BitVec(f'f{i}', 64) for i in range(flag_length)]
    
    #z3 optimisation
    for var in flag_vars:
        solver.add(var >= 30)
        solver.add(var <= 127)
    
    known_values = [ord('i'), ord('c'), ord('t'), ord('f'), ord('{')]
    for i in range(len(known_values)):
        solver.add(flag_vars[i] == known_values[i])
    solver.add(flag_vars[-1] == ord('}'))
    
    c_out = create_constraints(flag_vars)
    assert(len(c_out) == len(answer))

    for i in range(len(c_out)):
        solver.add(answer[i] == c_out[i])

    if solver.check() == sat:
        model = solver.model()
        flag = [chr(model.eval(flag_vars[i]).as_long()) for i in range(flag_length)]
        return ''.join(flag)
    else:
        return "No solution found."

answer = [
    0x348A627D10659, 0x27485A840365FE61, 0x9E735DADF26D31CD,
    0x82714BC9F9B579D9, 0x3DFB7CC801D16BC9, 0x602A04EFE5DAD659,
    0x0EB801D915A30D3D, 0x217DBE10EDCB20A1, 0x0ADEE2637E875CA19,
    0x0CD44AED238E9871, 0x0D3BFF76AE6B504D, 0x7181426EFF59E789,
    0x477616CB20C2DAC9, 0x0CE1206E1E46CE4A9, 0x946E7CB964A3F87D,
    0x499607CBF0C3291, 0x6871D4372347C759, 0x75412F56B7D8B01,
    0x0F8E57C264786E34D, 0x194CA6020EC505B9, 0x3E1A22E34FE84949,
    0x0A46DE25172742B79, 0x0CD0E971BCBFE6E3D, 0x56561961138A2501,
    0x78D2B538AB53CA19, 0x0A9980CA75AB6D611, 0x5F81576B5D4716CD,
    0x17B9860825B93469, 0x0C012F75269298349, 0x17373EE9C7A3AAC9,
    0x0B2E50798B11E1A7D, 0x0ADA5A6562E0FD7F1, 0x0EC3D9A68F1C99E59,
    0x3D828B35505D79A1, 0x0F76E5264F7BD16CD, 0x0DD230B3EC48ED399,
    0x80D93363DCD354C9, 0x7031567681E76299, 0x8977338CD4E2A93D,
    0x8A5708A1D4C02B61, 0x2066296A21501019, 0x9E260D94A4D775B1,
    0x0E7667BBD72280F4D, 0x12DF4035E1684349
]

print(solve_flag(answer))

On obtient donc le flag : ictf{i_l0ve_interp0lati0n_2ca38d6ef0a709e0}