TCTF 2024 - Functions
On nous fournit un binaire : main
Malgré le fait qu’il soit tag facile, ce challenge fut le moins solve de tout les challs reverse.
Analyse du binaire
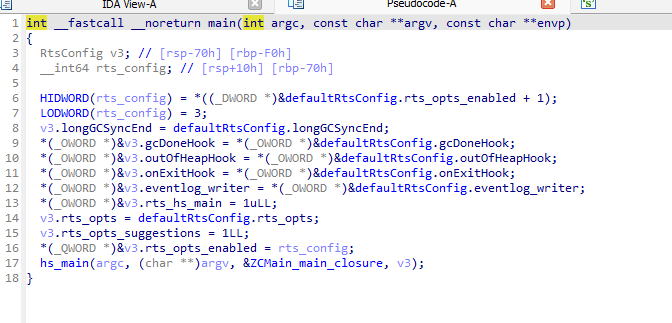
Bon cette signature de fonction, ainsi que le nom manglé de beaucoup de fonctions à coté sont typique du langage haskell. Haskell étant un language fonctionnel et qui est compilé avec ghc (Glasgow Haskell Compiler). Le reverse de ce genre de programme n’est pas aisé, et souvent trop compliqué manuellement (et je n’avais que 4h avant de partir).
j’ai donc téléchargé le tool hsdecomp qui est un tool pour tenter de reconstruire le code fonctionnel à partir du binaire.
Patch
Bon déja malheuresement le tool est vieux (6ans), on peut tenter de le run mais on va avoir ce genre d’erreur :
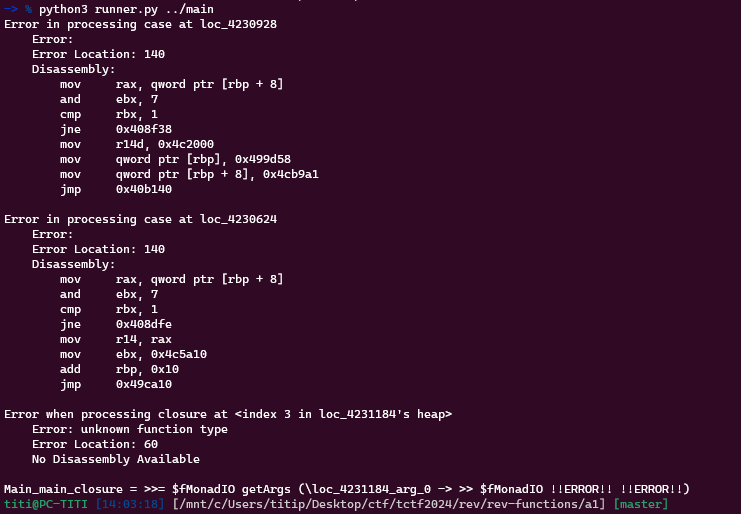
comment on peut le voir, le tool essaye de descendre dans les noeuds du code fonctionnel à partir d’un point d’entrée (ici Main_main_closure, qui est le main() d’un programme haskell)
On voit qu’il va appeler le getArgs avec un argument mais après c’est erreur sur erreur (il ne continue pas sa descente).
Tentons de trouver des forks qui serait plus récent, on peut notamment prendre celui la : https://github.com/oldkingOK/hsdecomp qui a update des tables pour des versions récentes de ghc.
on a maintenant :
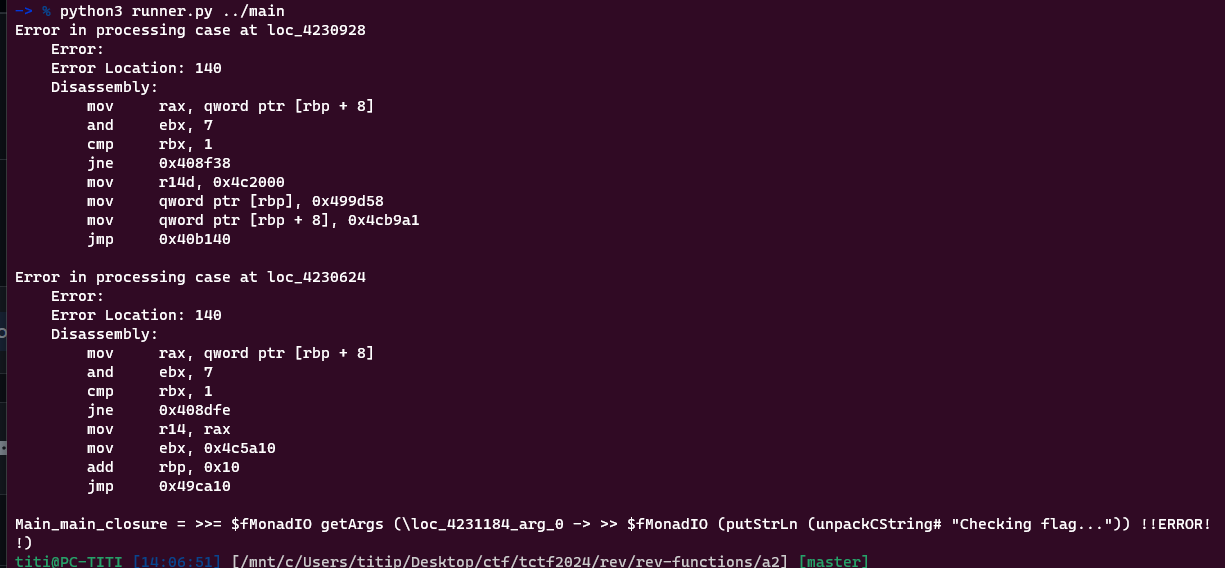
Ok c’est presque mieux, on voit la référence à CheckingFlag, le tout premier string affiché dans le programme lors de son éxécution, mais rien de concluant….
Tentons de patcher le tool pour afficher le reste même si un noeud est incorrect.
La première erreur vient du fait que le tool attend lors de l’analyse d’une fonction/case que le jump soit un jae (jump if condition is meet), mais dans notre version du programme, nous avons d’autre branch. on peut patcher ceci de manière sauvage :
diff --git a/hsdecomp/parse/__init__.py b/hsdecomp/parse/__init__.py
index 1a7e86d..f5f39f2 100644
--- a/hsdecomp/parse/__init__.py
+++ b/hsdecomp/parse/__init__.py
@@ -96,7 +96,8 @@ def gather_case_arms(settings, heaps, address, min_tag, max_tag, initial_stack,
mach.simulate(first_instructions)
if first_instructions[-2].mnemonic == 'cmp' and isinstance(mach.load(first_instructions[-2].operands[0]), Tagged) and isinstance(mach.load(first_instructions[-2].operands[0]).untagged, Offset) and isinstance(mach.load(first_instructions[-2].operands[0]).untagged.base, CasePointer) and first_instructions[-2].operands[1].type == capstone.x86.X86_OP_IMM:
- assert first_instructions[-1].mnemonic == 'jae'
+
+ #assert (first_instructions[-1].mnemonic == 'jae')
small_address = sum(map(lambda insn: insn.size, first_instructions)) + address
large_address = first_instructions[-1].operands[0].imm
Nous avons également le parsing plus loin d’une fonction qui fail, mais elle n’est pas importante et bloque la reconstruction du programme. On peut virer un assert pour continuer :
diff --git a/hsdecomp/infer.py b/hsdecomp/infer.py
index 6780946..0f06302 100644
--- a/hsdecomp/infer.py
+++ b/hsdecomp/infer.py
@@ -60,7 +60,7 @@ def rename_tags(settings, interps, types, interp):
seen_tags[tag.value] = None
interp.tags[i] = NamedTag(name = scrut_ty.constructor_names[tag.value], value = tag.value)
if scrut_ty.complete and len(interp.tags) == len(scrut_ty.constructor_names):
- assert len(seen_tags) == len(scrut_ty.constructor_names) - 1
+ #assert len(seen_tags) == len(scrut_ty.constructor_names) - 1
for i in range(len(interp.tags)):
if not i+1 in seen_tags:
missing_tag = i+1
Nous avons maintenant cette sortie :
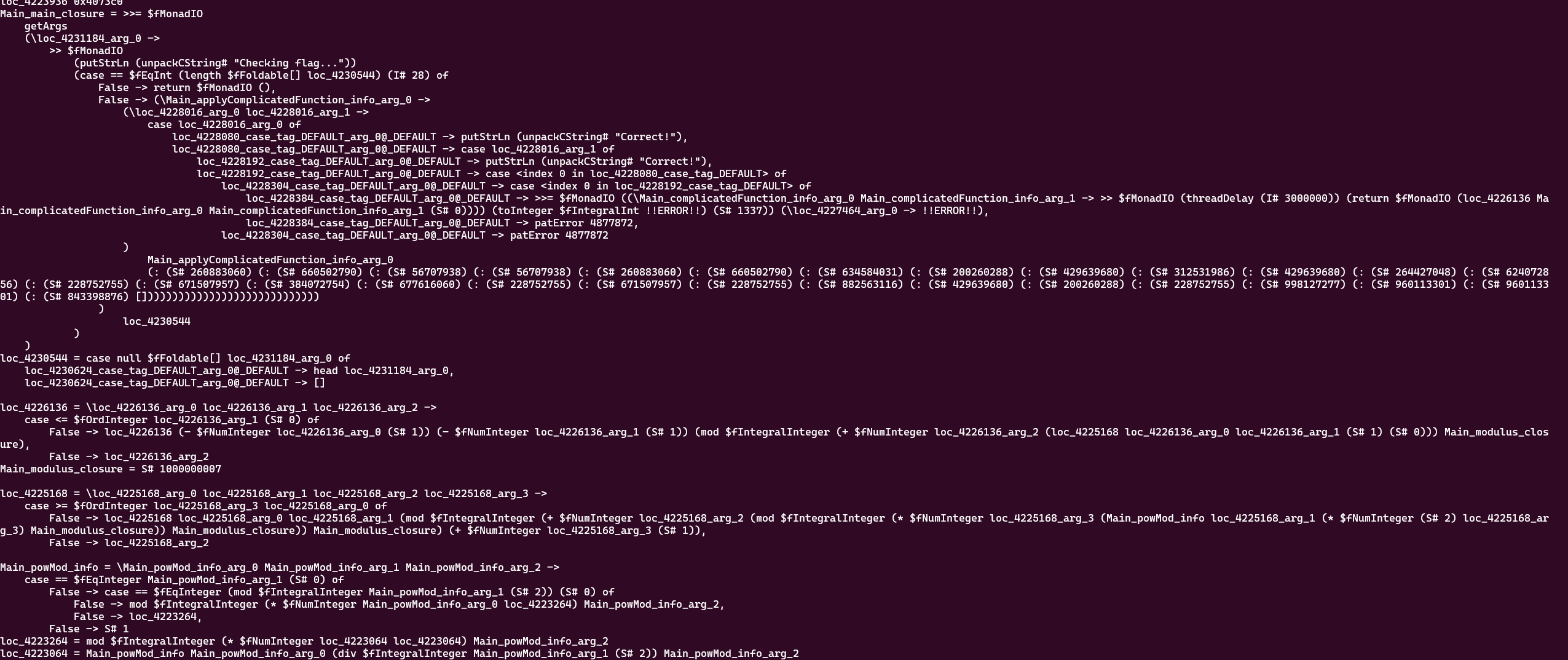
c’est bien mieux
Reconstruction du programme
On a en analysant le programme fonctionnel (symbole resymbolisé, pas les noms précis sauf pour certaines fonctions):
Main -> getArgs argv ->(putStrLn (unpackCString# "Checking flag...")) ->
(case == $fEqInt (length $fFoldable[] check_empty) (I# 28) of False -> return $fMonadIO (), //test if flag==28
True -> Main_applyComplicatedFunction_info(argv)
-> case True -> putStrLn (unpackCString# "Correct!"),
-> case False -> putStrLn (unpackCString# "Incorrect!"),
avec :
check_empty = case null $fFoldable[] a1 of
loc_4230624_case_tag_DEFAULT_arg_0@_DEFAULT -> head a1,
loc_4230624_case_tag_DEFAULT_arg_0@_DEFAULT -> []
(teste juste si l'entrée est vide ou non)
On a donc le flag de taille 28, vu avec le check de la taille au début
Pour Main_applyComplicatedFunction_info on va avoir :
loc_4228304_case_tag_DEFAULT_arg_0@_DEFAULT -> case <index 0 in loc_4228192_case_tag_DEFAULT> of
loc_4228384_case_tag_DEFAULT_arg_0@_DEFAULT -> >>= $fMonadIO ((\Main_complicatedFunction_info_arg_0 Main_complicatedFunction_info_arg_1 -> >> $fMonadIO (threadDelay (I# 3000000)) (return $fMonadIO (ComplicatedFunction Main_complicatedFunction_info_arg_0 Main_complicatedFunction_info_arg_1 (S# 0)))) (toInteger $fIntegralInt !!ERROR!!) (S# 1337)) (\loc_4227464_arg_0 -> !!ERROR!!),
Bon dans toute cette horreur de reconstruction, l’éssentiel qu’il faut retenir est que le programme va appeler ComplicatedFunction avec en paramètre un byte du flag à chaque fois, la constante 1337 et l’accumulateur (utilisé dans les languages fonctionnel) en 3ème argument, qui a été guess à 0 (comme très souvent) :
for i in range(28):
r = ComplicatedFunction(flag[i], 1337, 0)
if r == answer[i]:
continue
else:
fail()
ok()
avec answer l’array que l’on peut obtenir dans le code reconstruit :
(: (S# 260883060) (: (S# 660502790) (: (S# 56707938) (: (S# 56707938) (: (S# 260883060) (: (S# 660502790) (: (S# 634584031) (: (S# 200260288) (: (S# 429639680) (: (S# 312531986) (: (S# 429639680) (: (S# 264427048) (: (S# 624072856) (: (S# 228752755) (: (S# 671507957) (: (S# 384072754) (: (S# 677616060) (: (S# 228752755) (: (S# 671507957) (: (S# 228752755) (: (S# 882563116) (: (S# 429639680) (: (S# 200260288) (: (S# 228752755) (: (S# 998127277) (: (S# 960113301) (: (S# 960113301) (: (S# 843398876) []))))))))))))))))))))))))))))
Il faut donc maintenant comprendre ce que fait ComplicatedFunction:
Main_modulus_closure = S# 1000000007
ComplicatedFunction = \ComplicatedFunction_arg_0 ComplicatedFunction_arg_1 ComplicatedFunction_arg_2 ->
case <= $fOrdInteger ComplicatedFunction_arg_1 (S# 0) of
False -> ComplicatedFunction (- $fNumInteger ComplicatedFunction_arg_0 (S# 1)) (- $fNumInteger ComplicatedFunction_arg_1 (S# 1)) (mod $fIntegralInteger (+ $fNumInteger ComplicatedFunction_arg_2 (helper_function ComplicatedFunction_arg_0 ComplicatedFunction_arg_1 (S# 1) (S# 0))) Main_modulus_closure),
True -> ComplicatedFunction_arg_2
Donc nous avons le code suivant :
def complicated_function(x, y, acc):
if y <= 0:
return acc
else:
return complicated_function(
x - 1,
y - 1,
(acc + helper_function(x, y, 1, 0)) % MODULUS
)
Ici x correspond au byte du flag, y 1337 et acc l’accumulateur qui sera renvoyé lorsque y<= 0
En haskell, la fonction est appliqué avec les arguments qui se suivent :
Example : <= $fOrdInteger ComplicatedFunction_arg_1 (S# 0) , c’est un équivalent de if arg1 <= 0 {}
On peut également retrouver ce que font le reste des fonctions :
#nom reconstruit
helper_function = \x y a b ->
case >= $fOrdInteger b x of
False -> helper_function x y
(
mod $fIntegralInteger
(+ $fNumInteger a
(mod $fIntegralInteger
(* $fNumInteger b
(Main_powMod_info y
(* $fNumInteger
(S# 2) b
) Main_modulus_closure
)
) Main_modulus_closure
)
) Main_modulus_closure
)
(+ $fNumInteger b (S# 1)),
False -> a
#nom reconstruit
Main_powMod_info = \Main_powMod_info_arg_0 Main_powMod_info_arg_1 Main_powMod_info_arg_2 ->
case == $fEqInteger Main_powMod_info_arg_1 (S# 0) of
False -> case == $fEqInteger (mod $fIntegralInteger Main_powMod_info_arg_1 (S# 2)) (S# 0) of
False -> mod $fIntegralInteger (* $fNumInteger Main_powMod_info_arg_0 loc_4223264) Main_powMod_info_arg_2,
False -> loc_4223264,
False -> S# 1
loc_4223264 = mod $fIntegralInteger (* $fNumInteger loc_4223064 loc_4223064) Main_powMod_info_arg_2
loc_4223064 = Main_powMod_info Main_powMod_info_arg_0 (div $fIntegralInteger Main_powMod_info_arg_1 (S# 2)) Main_powMod_info_arg_2
ce qui donne en python par exemple :
def helper_function(x, y, a, b):
if b >= x:
return a
else:
return helper_function(
x, y,
(a + (b * pow_mod(y, 2 * b, MODULUS))) % MODULUS,
b + 1
)
def pow_mod(base, exp, modulus):
if exp == 0:
return 1
half_pow = pow_mod(base, exp // 2, modulus)
half_pow = (half_pow * half_pow) % modulus
if exp % 2 != 0:
return (half_pow * base) % modulus
return half_pow
Nous avons donc tout les éléments en main pour écrire un solver pour retrouver le flag :
MODULUS = 1000000007
import sys
sys.setrecursionlimit(11500) #important, sinon vous allez crash
specific_values = [
260883060, 660502790, 56707938, 56707938, 260883060, 660502790,
634584031, 200260288, 429639680, 312531986, 429639680, 264427048,
624072856, 228752755, 671507957, 384072754, 677616060, 228752755,
671507957, 228752755, 882563116, 429639680, 200260288, 228752755,
998127277, 960113301, 960113301, 843398876
]
def complicated_function(x, y, acc):
if y <= 0:
return acc
else:
return complicated_function(
x - 1,
y - 1,
(acc + helper_function(x, y, 1, 0)) % MODULUS
)
def helper_function(x, y, a, b):
if b >= x:
return a
else:
return helper_function(
x, y,
(a + (b * pow_mod(y, 2 * b, MODULUS))) % MODULUS,
b + 1
)
def pow_mod(base, exp, modulus):
if exp == 0:
return 1
half_pow = pow_mod(base, exp // 2, modulus)
half_pow = (half_pow * half_pow) % modulus
if exp % 2 != 0:
return (half_pow * base) % modulus
return half_pow
flag = ""
for i in range(28):
for ch in range(0xff):
z = complicated_function(ch, 1337, 0)
if z == specific_values[i]:
flag += chr(ch)
break
print(flag)
//TFCCTF{timing_are_a_bit_off}